三角形の面積は言うまでもなく底辺の長さと高さを掛けたものの半分である。
あらゆる三角形は平行四辺形の面積の半分だからだ。
ところで、高さが同じ三角形で底辺の長さが同じなら残りの二辺の長さがいくらであっても面積が同じになる(等積変形)ことはユークリッド原論にある。
また、その論の延長で、底辺の長さが元の倍になれば、高さが一定なら面積も倍になる。

この図は等積変形を示している。
直線mと直線nは平行である(m//n)。
底辺ABが共通の△ABDと△ABEの面積は等しい。なぜなら高さが同じだからだ。
さらに底辺を倍にした△ACEの面積は△ABDの倍になる。
三角形の底辺の長さとその面積は比例することを等積変形の定理は示している。
初等幾何学において等積変形や三角形の相似および合同を使った問題が多く出題される。
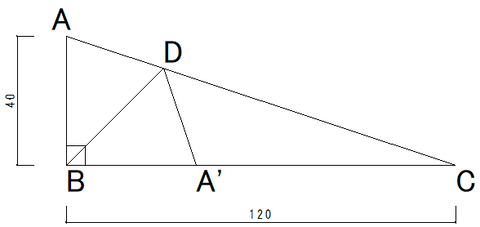
たとえばこのような問題である。
直角三角形ABCの頂点Aを辺BC上に来るように折り曲げると、辺BDを境界にして点A'ができる。
この場合の△A'CDの面積を求めよというものだ。
△ABD≡△A'BD
AB=BA'=4cm
折り曲げただけの図形だから当然だろう。
すると、A'C=12-4=8cmであることも明白である。
ここで等積変形の考えを用いるのだった。
BA':A'C=4:8=1:2
という共通底辺の長さの比であることと、頂点Dが共通の△BA'Dと△A'CDより高さが不明でも相等しいことがわかる。
△ABCの面積(12×4/2=24㎠)から△ABDと△A'BD(合同)の面積を引いてやればよいのだが、その面積が不明だ。
ところが△A'CDの面積は△ABDの二倍であることが等積変形からわかるので、結局△ABDの面積は△ABCの4分の1であることが判明する。
そうであれば、△A'CDの面積は△ABCの面積の半分であることがたちどころにわかる。
解答は、24/2=12㎠となる。
もう一題はこういう問題だ。

長方形ABCDの内部で△AED=13㎠、△AEB=19㎠、△BEC=17㎠のとき、残る△CDEの面積はいくらか?
これも等積変形ですぐに解けてしまう。
手掛かりは、長方形の辺ADと辺BCが平行であることだ。
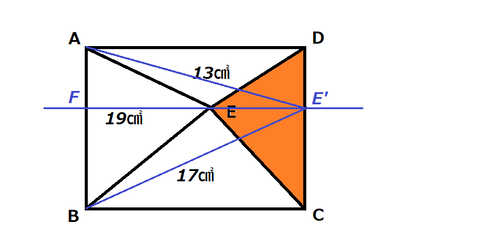
ADに平行な点Eを通る直線FE'を補助線として引く。そうすると点EがE'に移動しても、△AEDの面積は△AE'Dに等積変形される。同様に、△BECも△BE'Cに等積変形されるだろう。
見えてきたのは、新たな長方形AFE'Dと長方形BFE'Cであり、それぞれの対角線AE'とBE'によって面積既知の直角三角形に二分されているではないか?
これで長方形ABCDの面積が13×2+17×2=60㎠と判明する。
そうであれば、△CDEの面積は60-(13+19+17)=11㎠となるはずだ。
次の問題も等積変形の応用と言える。
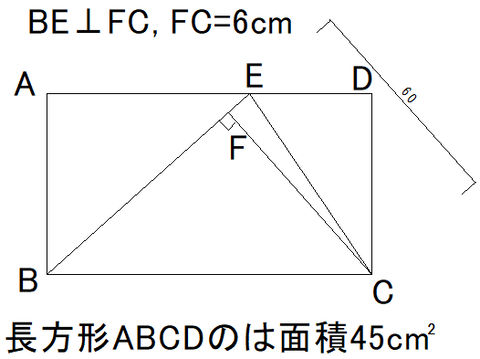
このときにBEの長さを求めよという問題だ。
点EをDに移動して△BCEを等積変形してみる。
すると△BCEの面積は長方形ABCDの面積の半分であることがすぐにわかる。
△BCEの面積は求める長さBEを底辺とすれば、
BE×FC/2
であり、FCは6㎝と与えられているから、
45㎠/2=6×BE/2
6×BE=45
BE=7.5cm
と求まる。
あらゆる三角形は平行四辺形の面積の半分だからだ。
ところで、高さが同じ三角形で底辺の長さが同じなら残りの二辺の長さがいくらであっても面積が同じになる(等積変形)ことはユークリッド原論にある。
また、その論の延長で、底辺の長さが元の倍になれば、高さが一定なら面積も倍になる。

この図は等積変形を示している。
直線mと直線nは平行である(m//n)。
底辺ABが共通の△ABDと△ABEの面積は等しい。なぜなら高さが同じだからだ。
さらに底辺を倍にした△ACEの面積は△ABDの倍になる。
三角形の底辺の長さとその面積は比例することを等積変形の定理は示している。
初等幾何学において等積変形や三角形の相似および合同を使った問題が多く出題される。

たとえばこのような問題である。
直角三角形ABCの頂点Aを辺BC上に来るように折り曲げると、辺BDを境界にして点A'ができる。
この場合の△A'CDの面積を求めよというものだ。
△ABD≡△A'BD
AB=BA'=4cm
折り曲げただけの図形だから当然だろう。
すると、A'C=12-4=8cmであることも明白である。
ここで等積変形の考えを用いるのだった。
BA':A'C=4:8=1:2
という共通底辺の長さの比であることと、頂点Dが共通の△BA'Dと△A'CDより高さが不明でも相等しいことがわかる。
△ABCの面積(12×4/2=24㎠)から△ABDと△A'BD(合同)の面積を引いてやればよいのだが、その面積が不明だ。
ところが△A'CDの面積は△ABDの二倍であることが等積変形からわかるので、結局△ABDの面積は△ABCの4分の1であることが判明する。
そうであれば、△A'CDの面積は△ABCの面積の半分であることがたちどころにわかる。
解答は、24/2=12㎠となる。
もう一題はこういう問題だ。

長方形ABCDの内部で△AED=13㎠、△AEB=19㎠、△BEC=17㎠のとき、残る△CDEの面積はいくらか?
これも等積変形ですぐに解けてしまう。
手掛かりは、長方形の辺ADと辺BCが平行であることだ。

ADに平行な点Eを通る直線FE'を補助線として引く。そうすると点EがE'に移動しても、△AEDの面積は△AE'Dに等積変形される。同様に、△BECも△BE'Cに等積変形されるだろう。
見えてきたのは、新たな長方形AFE'Dと長方形BFE'Cであり、それぞれの対角線AE'とBE'によって面積既知の直角三角形に二分されているではないか?
これで長方形ABCDの面積が13×2+17×2=60㎠と判明する。
そうであれば、△CDEの面積は60-(13+19+17)=11㎠となるはずだ。
次の問題も等積変形の応用と言える。

このときにBEの長さを求めよという問題だ。
点EをDに移動して△BCEを等積変形してみる。
すると△BCEの面積は長方形ABCDの面積の半分であることがすぐにわかる。
△BCEの面積は求める長さBEを底辺とすれば、
BE×FC/2
であり、FCは6㎝と与えられているから、
45㎠/2=6×BE/2
6×BE=45
BE=7.5cm
と求まる。
コメント